8 Tutorial: Data analysis with tidycomm

After working through Tutorial 8, you’ll…

  • understand how to install a package from GitHub instead of CRAN.
  • learn how to use the tidycomm package to perform descriptive analyses and run significance tests.
  • get a first glimpse into quick visualizations of your significance tests using tidycomm.

8.1 Installing a package from GitHub

In this part of the tutorial, we’re going to learn how to install R packages directly from GitHub, specifically from a development branch named devel.

Why might we want to do this? There are several reasons. Often, the most recent and innovative features of a package are found in these development branches. Developers use these branches to try out new features and fix bugs before merging them into the main branch that will be deployed via CRAN. By installing from the devel branch, you can access the latest features and updates ahead of their official release. It’s like a sneak peek into the future of the package!

However, it’s important to note that because these branches are under development, they might be unstable or have unaddressed issues. Hence, these versions are recommended for users who want to try the latest features or for those who are involved in the development of the package.

Now, let’s dive in and learn how to install the tidycomm package from the devel branch on GitHub. As a Windows user, you will need to install RTools 4.3 for Windows. As a Mac user, you might need to install Xcode. But I don’t have prior experience in package development on Mac. After that, install and load the devtools package, a package that supports R package development. In addition, install and load the remotes package, which allows you to install packages from Github.

# install.packages("devtools") # run only the first time
# install.packages("remotes") # run only the first time
library(devtools)
library(remotes)

Next, navigate to Julian Unkel’s Github repository that stores tidycomm in your internet browser. Here you can see that Julian has several branches in this repository, one of which is called devel.

To install the tidycomm package from this devel branch, use the install.github function from the remotes package. Provide the GitHub username, the repository name, and the branch name as follows:

remotes::install_github("joon-e/tidycomm@devel")
# Alternatively, you can use this code: remotes::install_github("joon-e/tidycomm", ref="devel")

Then, load the package:

library(tidycomm)

Finally, load the WoJ and the fbposts data:

WoJ <- tidycomm::WoJ
fbposts <- tidycomm::fbposts

The tidycomm package provides convenience functions for common data modification and analysis tasks in communication research. This includes functions for univariate and bivariate data analysis, index generation and reliability computation, and intercoder reliability tests.

8.2 Compute intercoder reliability

You can use tidycomm for your content analyses projects. The test_icr function performs an intercoder reliability test by computing various intercoder reliability estimates (e.g., Krippendorff’s alpha, Cohen’s kappa) for the included variables. If no variables are specified, the function will compute for all variables in the data set (excluding the unit_var and coder_var).

Let’s take a quick look at the fbposts data set that comes pre-packaged with tidycomm. It’s a coder-annotated data set, with each Facebook post (post_id) annotated by several coders (coder_id).

fbposts
## # A tibble: 270 × 7
##    post_id coder_id type  n_pictures pop_elite pop_people pop_othering
##      <int>    <int> <chr>      <int>     <int>      <int>        <int>
##  1       1        1 photo          1         0          0            0
##  2       1        2 photo          1         0          0            0
##  3       1        3 photo          1         0          0            0
##  4       1        4 photo          1         0          0            0
##  5       1        5 photo          1         0          0            0
##  6       1        6 photo          1         0          0            0
##  7       2        1 photo          1         0          0            0
##  8       2        2 photo          1         0          0            0
##  9       2        3 photo          1         0          0            0
## 10       2        4 photo          1         0          0            0
## # ℹ 260 more rows

Next, let’s calculate intercoder reliability estimates for each variable in the fbposts data set, excluding post_id and coder_id. The output includes simple percent agreement, Holsti’s reliability estimate (mean pairwise agreement), and Krippendorff’s Alpha by default, but you can specify other estimates to compute via optional arguments / parameters.

fbposts %>% test_icr(post_id, coder_id)
## # A tibble: 5 × 8
##   Variable     n_Units n_Coders n_Categories Level   Agreement Holstis_CR
## * <chr>          <int>    <int>        <int> <chr>       <dbl>      <dbl>
## 1 type              45        6            4 nominal     1          1    
## 2 n_pictures        45        6            7 nominal     0.822      0.930
## 3 pop_elite         45        6            6 nominal     0.733      0.861
## 4 pop_people        45        6            2 nominal     0.778      0.916
## 5 pop_othering      45        6            4 nominal     0.867      0.945
## # ℹ 1 more variable: Krippendorffs_Alpha <dbl>

Here are some more ICR estimates:

fbposts %>% test_icr(post_id, coder_id,
  fleiss_kappa = TRUE,
  lotus = TRUE
)
## # A tibble: 5 × 10
##   Variable     n_Units n_Coders n_Categories Level   Agreement Holstis_CR
## * <chr>          <int>    <int>        <int> <chr>       <dbl>      <dbl>
## 1 type              45        6            4 nominal     1          1    
## 2 n_pictures        45        6            7 nominal     0.822      0.930
## 3 pop_elite         45        6            6 nominal     0.733      0.861
## 4 pop_people        45        6            2 nominal     0.778      0.916
## 5 pop_othering      45        6            4 nominal     0.867      0.945
## # ℹ 3 more variables: Krippendorffs_Alpha <dbl>, Fleiss_Kappa <dbl>,
## #   Lotus <dbl>

8.3 How to run descriptive analyses

Dieser Teil des Tutorials ist aus meinen Vorbereitungen für die interne Mitarbeitendenfortbildung übernommen und daher auf Englisch.

8.3.1 Index generation

The tidycomm package provides a workflow to quickly add mean/sum indices of variables to the dataset and compute reliability estimates for those added indices. The package offers two key functions:

  1. add_index() and
  2. get_reliability()

8.3.1.1 add_index():

The add_index() function adds a mean or sum index of the specified variables to the data. The second argument (or first, if used in a pipe) is the name of the index variable to be created. For example, if you want to create a mean index named ‘ethical_concerns’ using variables ‘ethics_1’ to ‘ethics_4’, you can use the following code:

WoJ %>%
  add_index(ethical_concerns, ethics_1, ethics_2, ethics_3, ethics_4) %>%
  dplyr::select(ethical_concerns, 
                ethics_1, 
                ethics_2, 
                ethics_3, 
                ethics_4)
## # A tibble: 1,200 × 5
##    ethical_concerns ethics_1 ethics_2 ethics_3 ethics_4
##               <dbl>    <dbl>    <dbl>    <dbl>    <dbl>
##  1             2           2        3        2        1
##  2             1.5         1        2        2        1
##  3             2.25        2        4        2        1
##  4             1.75        1        3        1        2
##  5             2           2        3        2        1
##  6             3.25        2        4        4        3
##  7             2           1        3        2        2
##  8             3.5         2        4        4        4
##  9             1.75        1        2        1        3
## 10             3.25        1        4        4        4
## # ℹ 1,190 more rows

To create a sum index instead, set type = "sum":

WoJ %>%
  add_index(ethical_flexibility, ethics_1, ethics_2, ethics_3, ethics_4, type = "sum") %>% 
  dplyr::select(ethical_flexibility, 
                ethics_1, 
                ethics_2, 
                ethics_3, 
                ethics_4)
## # A tibble: 1,200 × 5
##    ethical_flexibility ethics_1 ethics_2 ethics_3 ethics_4
##                  <dbl>    <dbl>    <dbl>    <dbl>    <dbl>
##  1                   8        2        3        2        1
##  2                   6        1        2        2        1
##  3                   9        2        4        2        1
##  4                   7        1        3        1        2
##  5                   8        2        3        2        1
##  6                  13        2        4        4        3
##  7                   8        1        3        2        2
##  8                  14        2        4        4        4
##  9                   7        1        2        1        3
## 10                  13        1        4        4        4
## # ℹ 1,190 more rows

Make sure to save your index back into your original data set if you want to keep it for later use:

WoJ <- WoJ %>%
  add_index(ethical_concerns, ethics_1, ethics_2, ethics_3, ethics_4)

8.3.1.2 get_reliability()

The get_reliability() function computes reliability/internal consistency estimates for indices created with add_index(). The function outputs Cronbach’s α along with descriptives and index information.

WoJ %>% get_reliability(ethical_concerns)
## # A tibble: 1 × 5
##   Index            Index_of                              M    SD Cronbachs_Alpha
## * <chr>            <chr>                             <dbl> <dbl>           <dbl>
## 1 ethical_concerns ethics_1, ethics_2, ethics_3, et…  2.45 0.777           0.612

By default, if you pass no further arguments to the function, it will automatically compute reliability estimates for all indices created with add_index() found in the data.

WoJ %>% get_reliability()
## # A tibble: 1 × 5
##   Index            Index_of                              M    SD Cronbachs_Alpha
## * <chr>            <chr>                             <dbl> <dbl>           <dbl>
## 1 ethical_concerns ethics_1, ethics_2, ethics_3, et…  2.45 0.777           0.612

8.3.2 Rescaling of measures

Tidycomm provides four functions to easily transform continuous scales and to standardize them:

  • reverse_scale() simply turns a scale upside down
  • minmax_scale() down- or upsizes a scale to new minimum/maximum while retaining distances
  • center_scale() subtracts the mean from each individual data point to center a scale at a mean of 0
  • z_scale() works just like center_scale() but also divides the result by the standard deviation to also obtain a standard deviation of 1 and make it comparable to other z-standardized distributions
  • setna_scale() to define missing values
  • recode_cat_scale() to recode categrical variables into new categorical variables
  • categorize_scale() to turn a continoous variable into a categorical variable

8.3.2.1 reverse_scale()

The easiest one is to reverse your scale. You can just specify the scale and define the scale’s lower and upper end. Take autonomy_emphasis as an example that originally ranges from 1 to 5. We will reverse it to range from 5 to 1.

The function adds a new column named autonomy_emphasis_rev:

WoJ %>% 
  reverse_scale(autonomy_emphasis,
                lower_end = 1,
                upper_end = 5) %>% 
  dplyr::select(autonomy_emphasis,
                autonomy_emphasis_rev)
## # A tibble: 1,200 × 2
##    autonomy_emphasis autonomy_emphasis_rev
##                <dbl>                 <dbl>
##  1                 4                     2
##  2                 4                     2
##  3                 4                     2
##  4                 5                     1
##  5                 4                     2
##  6                 4                     2
##  7                 4                     2
##  8                 3                     3
##  9                 5                     1
## 10                 4                     2
## # ℹ 1,190 more rows

Alternatively, you can also specify the new column name manually:

WoJ %>% 
  reverse_scale(autonomy_emphasis,
                name = "new_emphasis",
                lower_end = 1,
                upper_end = 5) %>% 
  dplyr::select(autonomy_emphasis,
                new_emphasis)
## # A tibble: 1,200 × 2
##    autonomy_emphasis new_emphasis
##                <dbl>        <dbl>
##  1                 4            2
##  2                 4            2
##  3                 4            2
##  4                 5            1
##  5                 4            2
##  6                 4            2
##  7                 4            2
##  8                 3            3
##  9                 5            1
## 10                 4            2
## # ℹ 1,190 more rows

8.3.2.2 minmax_scale()

minmax_scale() just takes your continuous scale to a new range. For example, convert the 1-5 scale of autonomy_emphasis to a 1-10 scale while keeping the distances:

WoJ %>% 
  minmax_scale(autonomy_emphasis,
               change_to_min = 1,
               change_to_max = 10) %>% 
  dplyr::select(autonomy_emphasis,
                autonomy_emphasis_1to10)
## # A tibble: 1,200 × 2
##    autonomy_emphasis autonomy_emphasis_1to10
##                <dbl>                   <dbl>
##  1                 4                    7.75
##  2                 4                    7.75
##  3                 4                    7.75
##  4                 5                   10   
##  5                 4                    7.75
##  6                 4                    7.75
##  7                 4                    7.75
##  8                 3                    5.5 
##  9                 5                   10   
## 10                 4                    7.75
## # ℹ 1,190 more rows

8.3.2.3 center_scale()

center_scale() moves your continuous scale around a mean of 0:

WoJ %>% 
  center_scale(autonomy_selection) %>% 
  dplyr::select(autonomy_selection,
                autonomy_selection_centered)
## # A tibble: 1,200 × 2
##    autonomy_selection autonomy_selection_centered
##                 <dbl>                       <dbl>
##  1                  5                       1.12 
##  2                  3                      -0.876
##  3                  4                       0.124
##  4                  4                       0.124
##  5                  4                       0.124
##  6                  4                       0.124
##  7                  4                       0.124
##  8                  3                      -0.876
##  9                  5                       1.12 
## 10                  2                      -1.88 
## # ℹ 1,190 more rows

8.3.2.4 z_scale()

Moreover, z_scale() does more or less the same but standardizes the outcome. To visualize this, we look at it with a visualized tab_frequencies():

WoJ %>% 
  z_scale(autonomy_selection) %>% 
  tab_frequencies(autonomy_selection,
                  autonomy_selection_z) %>% 
  visualize()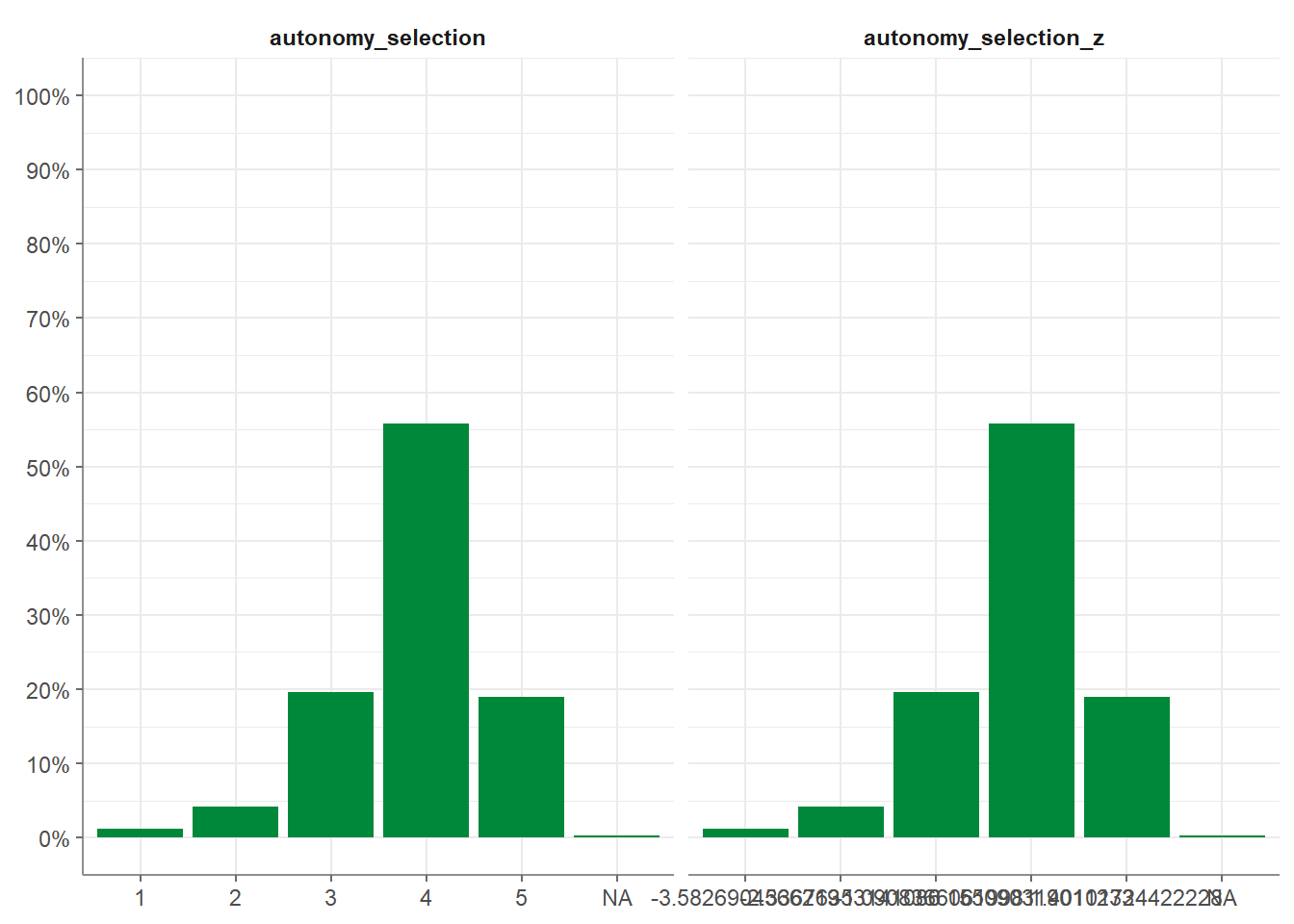

8.3.2.5 setna_scale()

To set a specific value to NA:

WoJ %>% 
  setna_scale(autonomy_emphasis, value = 5) %>% 
  dplyr::select(autonomy_emphasis, autonomy_emphasis_na)
## # A tibble: 1,200 × 2
##    autonomy_emphasis autonomy_emphasis_na
##                <dbl>                <dbl>
##  1                 4                    4
##  2                 4                    4
##  3                 4                    4
##  4                 5                   NA
##  5                 4                    4
##  6                 4                    4
##  7                 4                    4
##  8                 3                    3
##  9                 5                   NA
## 10                 4                    4
## # ℹ 1,190 more rows

8.3.2.6 recode_cat_scale()

For recoding categorical scales you can use recode_cat_scale():

WoJ %>% 
  dplyr::select(country) %>%
  recode_cat_scale(country, assign = c("Germany" = "german", "Switzerland" = "swiss"), other = "other")
## # A tibble: 1,200 × 2
##    country     country_rec
##  * <fct>       <fct>      
##  1 Germany     german     
##  2 Germany     german     
##  3 Switzerland swiss      
##  4 Switzerland swiss      
##  5 Austria     other      
##  6 Switzerland swiss      
##  7 Germany     german     
##  8 Denmark     other      
##  9 Switzerland swiss      
## 10 Denmark     other      
## # ℹ 1,190 more rows

Even if your original values are integers:

WoJ %>%
  select(ethics_1, ethics_2)  %>%
  recode_cat_scale(ethics_1, ethics_2,
                   assign = c(`1` = "very low", `2` = "low", `3` = "medium", `4` = "high", `5` = "very high"),
                   overwrite = TRUE)
## # A tibble: 1,200 × 2
##    ethics_1 ethics_2
##  * <fct>    <fct>   
##  1 low      medium  
##  2 very low low     
##  3 low      high    
##  4 very low medium  
##  5 low      medium  
##  6 low      high    
##  7 very low medium  
##  8 low      high    
##  9 very low low     
## 10 very low high    
## # ℹ 1,190 more rows

8.3.2.7 categorize_scale()

To recode numeric scales into categories:

WoJ %>%
  dplyr::select(autonomy_emphasis) %>%
  categorize_scale(autonomy_emphasis, 
               lower_end =1, upper_end =5,
               breaks = c(2, 3),
               labels = c("Low", "Medium", "High"))
## # A tibble: 1,200 × 2
##    autonomy_emphasis autonomy_emphasis_cat
##  *             <dbl> <fct>                
##  1                 4 High                 
##  2                 4 High                 
##  3                 4 High                 
##  4                 5 High                 
##  5                 4 High                 
##  6                 4 High                 
##  7                 4 High                 
##  8                 3 Medium               
##  9                 5 High                 
## 10                 4 High                 
## # ℹ 1,190 more rows

8.3.2.8 dummify_scale

And to create dummy variables:

WoJ %>% 
  dplyr::select(temp_contract) %>%
  dummify_scale(temp_contract)
## # A tibble: 1,200 × 3
##    temp_contract temp_contract_permanent temp_contract_temporary
##  * <fct>                           <int>                   <int>
##  1 Permanent                           1                       0
##  2 Permanent                           1                       0
##  3 Permanent                           1                       0
##  4 Permanent                           1                       0
##  5 Permanent                           1                       0
##  6 <NA>                               NA                      NA
##  7 Permanent                           1                       0
##  8 Permanent                           1                       0
##  9 Permanent                           1                       0
## 10 Permanent                           1                       0
## # ℹ 1,190 more rows

8.3.3 Univariate analysis

Univariate, descriptive analysis is usually the first step in data exploration. Tidycomm offers four basic functions to quickly output relevant statistics:

  1. describe(): For continuous variables
  2. tab_percentiles(): For continuous variables
  3. describe_cat(): For categorical variables
  4. tab_frequencies(): For categorical variables

8.3.3.1 Describe continuous variables

There are two options two describe continuous variables in tidycomm:

  1. describe() and
  2. tab_percentiles()

First, the describe() function outputs several measures of central tendency and variability for all variables named in the function call (i.e., mean, standard deviation, min, max, range, and quartiles). Here’s how you use it:

WoJ %>% describe(autonomy_emphasis, ethics_1, work_experience)
## # A tibble: 3 × 15
##   Variable            N Missing     M     SD   Min   Q25   Mdn   Q75   Max Range
## * <chr>           <int>   <int> <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 autonomy_empha…  1195       5  4.08  0.793     1     4     4     5     5     4
## 2 ethics_1         1200       0  1.63  0.892     1     1     1     2     5     4
## 3 work_experience  1187      13 17.8  10.9       1     8    17    25    53    52
## # ℹ 4 more variables: CI_95_LL <dbl>, CI_95_UL <dbl>, Skewness <dbl>,
## #   Kurtosis <dbl>

If no variables are passed to describe(), all numeric variables in the data are described:

WoJ %>% describe()
## # A tibble: 12 × 15
##    Variable           N Missing     M     SD   Min   Q25   Mdn   Q75   Max Range
##  * <chr>          <int>   <int> <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
##  1 autonomy_sele…  1197       3  3.88  0.803     1  4      4       4     5     4
##  2 autonomy_emph…  1195       5  4.08  0.793     1  4      4       5     5     4
##  3 ethics_1        1200       0  1.63  0.892     1  1      1       2     5     4
##  4 ethics_2        1200       0  3.21  1.26      1  2      4       4     5     4
##  5 ethics_3        1200       0  2.39  1.13      1  2      2       3     5     4
##  6 ethics_4        1200       0  2.58  1.25      1  1.75   2       4     5     4
##  7 work_experien…  1187      13 17.8  10.9       1  8     17      25    53    52
##  8 trust_parliam…  1200       0  3.05  0.811     1  3      3       4     5     4
##  9 trust_governm…  1200       0  2.82  0.854     1  2      3       3     5     4
## 10 trust_parties   1200       0  2.42  0.736     1  2      2       3     4     3
## 11 trust_politic…  1200       0  2.52  0.712     1  2      3       3     4     3
## 12 ethical_conce…  1200       0  2.45  0.777     1  2      2.5     3     5     4
## # ℹ 4 more variables: CI_95_LL <dbl>, CI_95_UL <dbl>, Skewness <dbl>,
## #   Kurtosis <dbl>

You can also group data (using dplyr) before describing:

WoJ %>%
  dplyr::group_by(country) %>%
  describe(autonomy_emphasis)
## # A tibble: 5 × 16
## # Groups:   country [5]
##   country Variable     N Missing     M    SD   Min   Q25   Mdn   Q75   Max Range
## * <fct>   <chr>    <int>   <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Austria autonom…   205       2  4.19 0.614     2     4     4     5     5     3
## 2 Denmark autonom…   375       1  3.90 0.856     1     4     4     4     5     4
## 3 Germany autonom…   172       1  4.34 0.818     1     4     5     5     5     4
## 4 Switze… autonom…   233       0  4.07 0.694     1     4     4     4     5     4
## 5 UK      autonom…   210       1  4.08 0.838     2     4     4     5     5     3
## # ℹ 4 more variables: CI_95_LL <dbl>, CI_95_UL <dbl>, Skewness <dbl>,
## #   Kurtosis <dbl>

Finally, you can create visualizations of your variables by applying the visualize() function to your data:

WoJ %>%
  describe(autonomy_emphasis) %>%
  visualize()

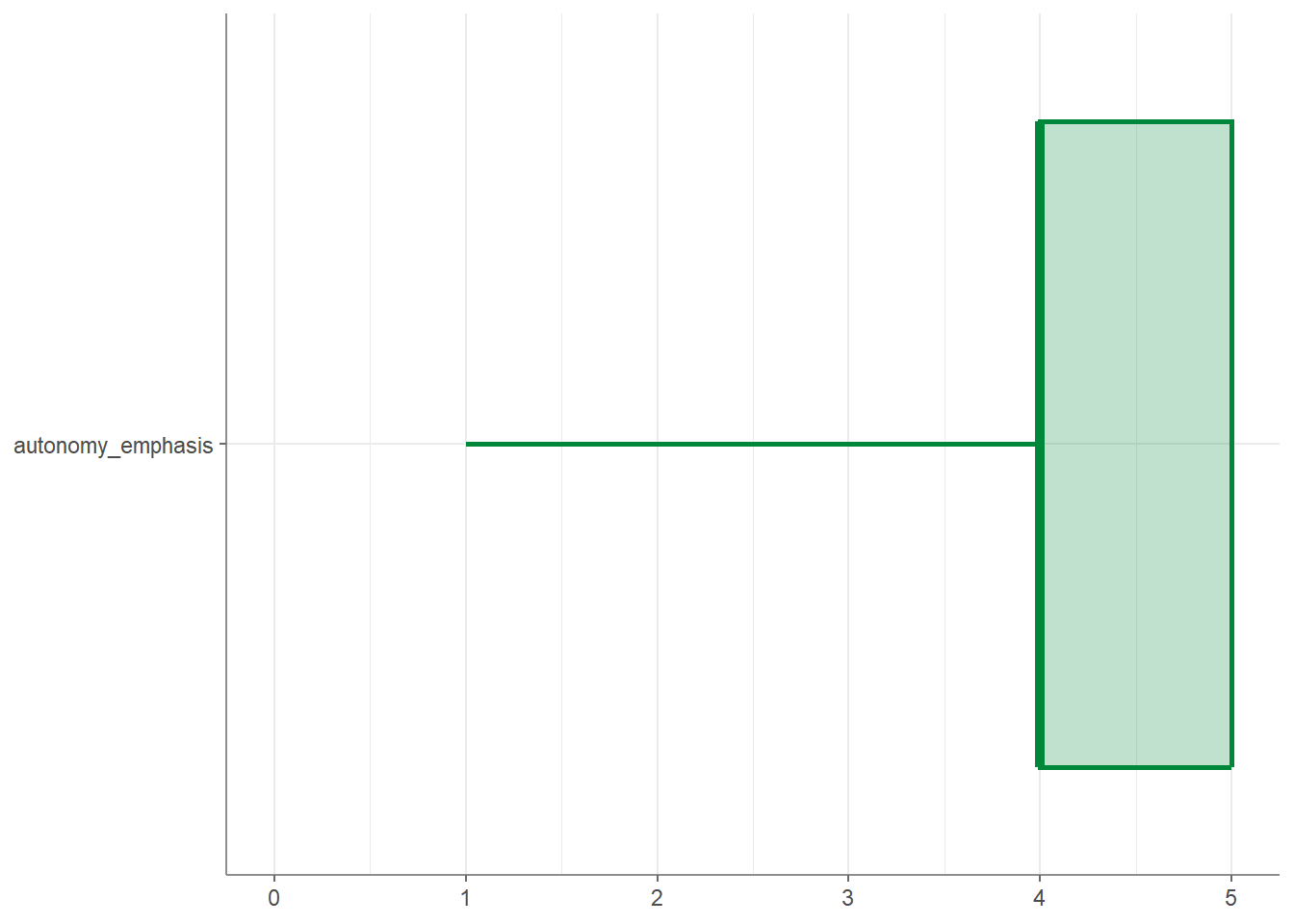
Second, the tab_percentiles function tabulates percentiles for at least one continuous variable:

WoJ %>%
  tab_percentiles(autonomy_emphasis)
## # A tibble: 1 × 11
##   Variable            p10   p20   p30   p40   p50   p60   p70   p80   p90  p100
## * <chr>             <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 autonomy_emphasis     3     4     4     4     4     4     4     5     5     5

You can use it to tabulate percentiles for more than one variable:

WoJ %>%
  tab_percentiles(autonomy_emphasis, ethics_1)
## # A tibble: 2 × 11
##   Variable            p10   p20   p30   p40   p50   p60   p70   p80   p90  p100
## * <chr>             <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 autonomy_emphasis     3     4     4     4     4     4     4     5     5     5
## 2 ethics_1              1     1     1     1     1     2     2     2     3     5

You can also specify your own percentiles:

WoJ %>%
  tab_percentiles(autonomy_emphasis, ethics_1, levels = c(0.16, 0.50, 0.84, 1.0))
## # A tibble: 2 × 5
##   Variable            p16   p50   p84  p100
## * <chr>             <dbl> <dbl> <dbl> <dbl>
## 1 autonomy_emphasis     3     4     5     5
## 2 ethics_1              1     1     2     5

And you can visualize your percentiles:

WoJ %>%
  tab_percentiles(autonomy_emphasis) %>%
  visualize()

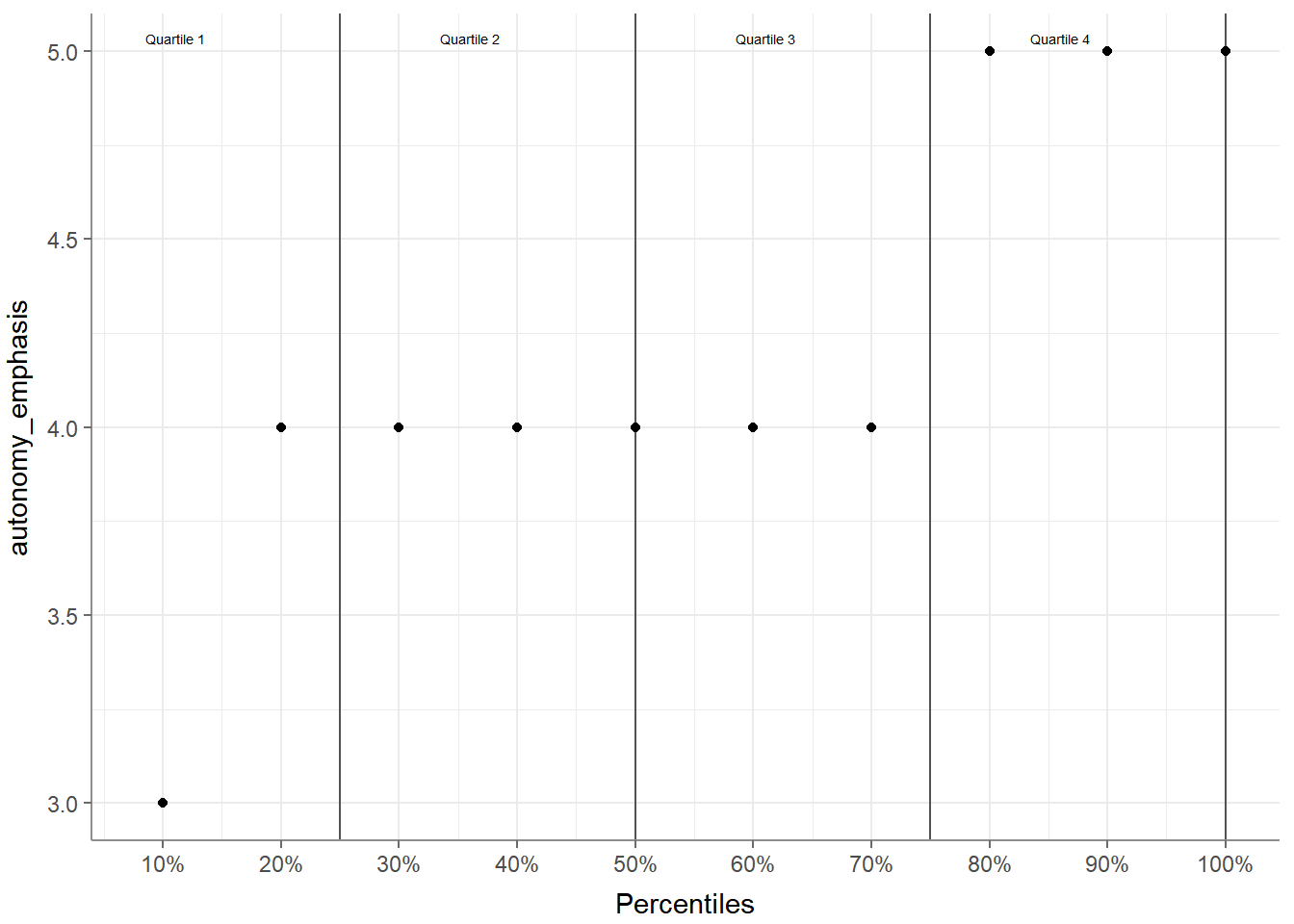
8.3.4 Bivariate analysis

You can perform a descriptive, bivariate analysis using the crosstab() function. The crosstab() function computes contingency tables for one independent (column) variable and one or more dependent (row) variables.

WoJ %>% crosstab(reach, employment)
## # A tibble: 3 × 5
##   employment Local Regional National Transnational
## * <chr>      <dbl>    <dbl>    <dbl>         <dbl>
## 1 Freelancer    23       36      104             9
## 2 Full-time    111      287      438            66
## 3 Part-time     15       32       75             4

You can also add a ‘Total’ column to the contingency table and output column-wise percentages instead of absolute values by using additional arguments:

WoJ %>% crosstab(reach, employment,
  add_total = TRUE,
  percentages = TRUE
)
## # A tibble: 3 × 6
##   employment Local Regional National Transnational Total
## * <chr>      <dbl>    <dbl>    <dbl>         <dbl> <dbl>
## 1 Freelancer 0.154   0.101     0.169        0.114  0.143
## 2 Full-time  0.745   0.808     0.710        0.835  0.752
## 3 Part-time  0.101   0.0901    0.122        0.0506 0.105

Finally, you can visualize your variables using the visualize() function:

WoJ %>%
  crosstab(reach, employment, chi_square = TRUE) %>%
  visualize()

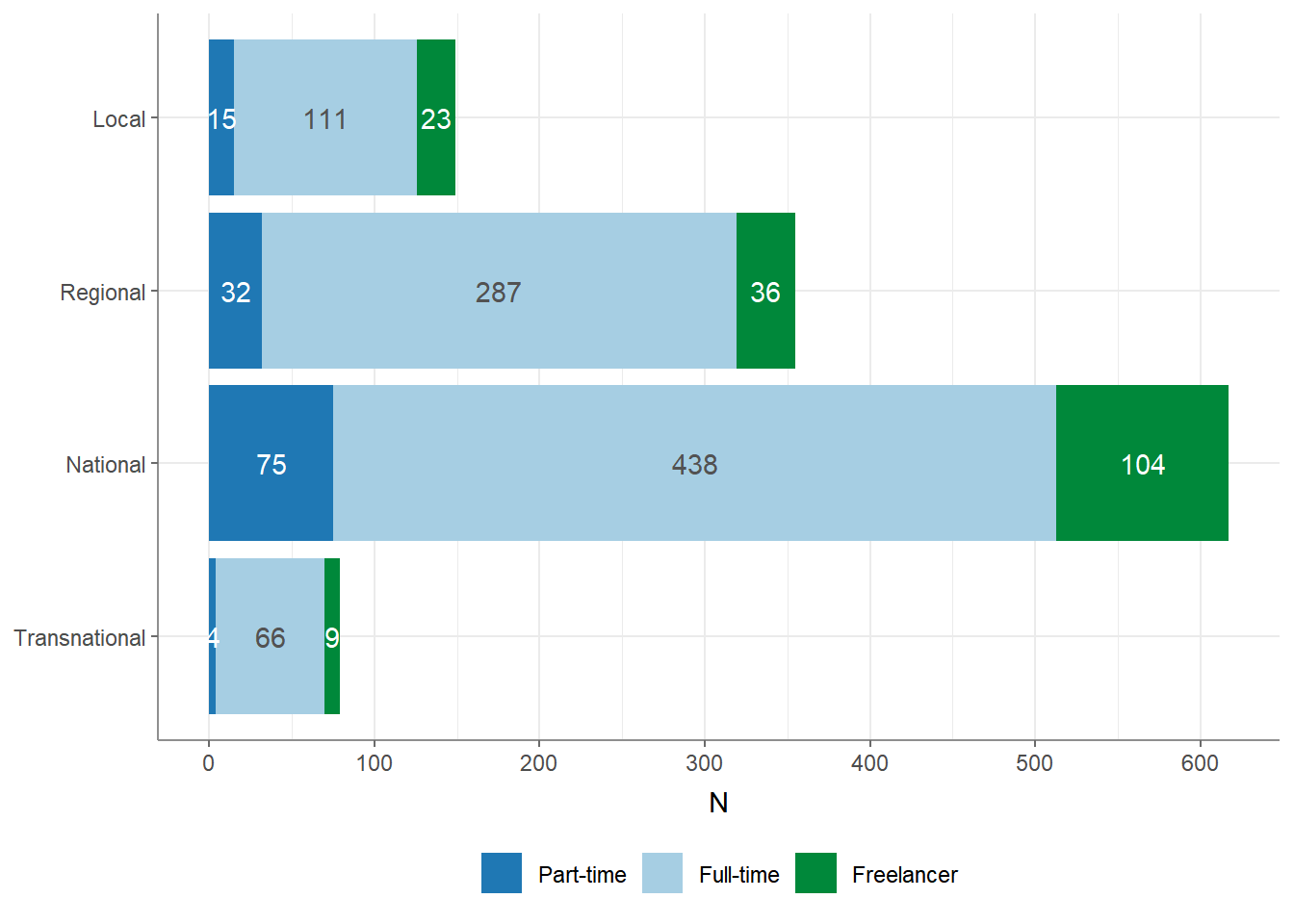
8.4 How to run significance tests

8.4.1 crosstab()

The ‘crosstab()’ function also offers a chi_square argument that, when set to TRUE, will calculate the chi-square test and Cramer’s V.

WoJ %>% crosstab(reach, employment, chi_square = TRUE)
## # A tibble: 3 × 5
##   employment Local Regional National Transnational
## * <chr>      <dbl>    <dbl>    <dbl>         <dbl>
## 1 Freelancer    23       36      104             9
## 2 Full-time    111      287      438            66
## 3 Part-time     15       32       75             4
## # Chi-square = 16.005, df = 6, p = 0.014, V = 0.082

Remember that you can access the full documentation of this function using the help() function, which will give you access to additional arguments / parameters and run examples of the function:

?crosstab()

8.4.2 t_test()

The t_test() function is used either to calculate a one-sample t-test or to compute t-tests for one group variable and specified test variables. If no variables are specified, all numeric (integer or double) variables are used. t_test() by default tests for equal variance (using a Levene test) to decide whether to use pooled variance or to use the Welch approximation to the degrees of freedom.

You can provide an independent (group) variable and a dependent variable and the t-values, p-values and Cohen’s d will be calculated.

WoJ %>% t_test(temp_contract, autonomy_emphasis)
## # A tibble: 1 × 12
##   Variable M_Permanent SD_Permanent M_Temporary SD_Temporary Delta_M     t    df
## * <chr>      <num:.3!>    <num:.3!>   <num:.3!>    <num:.3!> <num:.> <num> <dbl>
## 1 autonom…       4.124        0.768       3.887        0.870   0.237 2.171   995
## # ℹ 4 more variables: p <num:.3!>, d <num:.3!>, Levene_p <dbl>, var_equal <chr>

Remember that you can always save your analysis into an R object and inspect it with View(). This is very helpful if the resulting output is larger than your screen:

model1 <- WoJ %>% t_test(temp_contract, autonomy_emphasis)
View(model1)

You can also specify more than one dependent variable:

WoJ %>% t_test(temp_contract, autonomy_emphasis, ethics_1)
## # A tibble: 2 × 12
##   Variable      M_Permanent SD_Permanent M_Temporary SD_Temporary Delta_M      t
## * <chr>           <num:.3!>    <num:.3!>   <num:.3!>    <num:.3!> <num:.> <num:>
## 1 autonomy_emp…       4.124        0.768       3.887        0.870   0.237  2.171
## 2 ethics_1            1.568        0.850       1.981        0.990  -0.414 -3.415
## # ℹ 5 more variables: df <dbl>, p <num:.3!>, d <num:.3!>, Levene_p <dbl>,
## #   var_equal <chr>

If you do not specify a dependent variable, all suitable variables in your data set will be used:

WoJ %>% t_test(temp_contract)
## # A tibble: 12 × 12
##    Variable     M_Permanent SD_Permanent M_Temporary SD_Temporary Delta_M      t
##  * <chr>          <num:.3!>    <num:.3!>   <num:.3!>    <num:.3!> <num:.> <num:>
##  1 autonomy_se…       3.910        0.755       3.698        0.932   0.212  1.627
##  2 autonomy_em…       4.124        0.768       3.887        0.870   0.237  2.171
##  3 ethics_1           1.568        0.850       1.981        0.990  -0.414 -3.415
##  4 ethics_2           3.241        1.263       3.509        1.234  -0.269 -1.510
##  5 ethics_3           2.369        1.121       2.283        0.928   0.086  0.549
##  6 ethics_4           2.534        1.239       2.566        1.217  -0.032 -0.185
##  7 work_experi…      17.707       10.540      11.283       11.821   6.424  4.288
##  8 trust_parli…       3.073        0.797       3.019        0.772   0.054  0.480
##  9 trust_gover…       2.870        0.847       2.642        0.811   0.229  1.918
## 10 trust_parti…       2.430        0.724       2.358        0.736   0.072  0.703
## 11 trust_polit…       2.533        0.707       2.396        0.689   0.136  1.369
## 12 ethical_con…       2.428        0.772       2.585        0.774  -0.157 -1.443
## # ℹ 5 more variables: df <dbl>, p <num:.3!>, d <num:.3!>, Levene_p <dbl>,
## #   var_equal <chr>

If you have an independent (group) variable with more than two levels, you can also specify the levels that you want to use for your t_test():

WoJ %>% t_test(employment, autonomy_emphasis, levels = c("Full-time", "Freelancer"))
## # A tibble: 1 × 12
##   Variable `M_Full-time` `SD_Full-time` M_Freelancer SD_Freelancer Delta_M     t
## * <chr>        <num:.3!>      <num:.3!>    <num:.3!>     <num:.3!> <num:.> <num>
## 1 autonom…         4.118          0.781        3.901         0.852   0.217 3.287
## # ℹ 5 more variables: df <dbl>, p <num:.3!>, d <num:.3!>, Levene_p <dbl>,
## #   var_equal <chr>

Finally, t_test() by default tests for equal variance (using a Levene test) to decide whether to use pooled variance or to use the Welch approximation to the degrees of freedom. This is an example for the use of Welch’s approximation to account for unequal variances between groups:

WoJ %>% t_test(temp_contract, autonomy_selection)
## # A tibble: 1 × 12
##   Variable M_Permanent SD_Permanent M_Temporary SD_Temporary Delta_M     t    df
## * <chr>      <num:.3!>    <num:.3!>   <num:.3!>    <num:.3!> <num:.> <num> <dbl>
## 1 autonom…       3.910        0.755       3.698        0.932   0.212 1.627    56
## # ℹ 4 more variables: p <num:.3!>, d <num:.3!>, Levene_p <dbl>, var_equal <chr>

You can also run a one-sample t-test (also called: location test) by providing a variable and checking whether the mean of this variable is equal to a provided population mean mu:

WoJ %>% t_test(autonomy_selection, mu = 3)
## # A tibble: 1 × 9
##   Variable               M    SD CI_95_LL CI_95_UL    Mu     t    df         p
## * <chr>              <dbl> <dbl>    <dbl>    <dbl> <dbl> <dbl> <dbl>     <dbl>
## 1 autonomy_selection  3.88 0.803     3.83     3.92     3  37.7  1196 6.32e-206

Finally, you can visualize your test results by calling the visualize() function:

WoJ %>%
  t_test(temp_contract, autonomy_selection) %>%
  visualize()

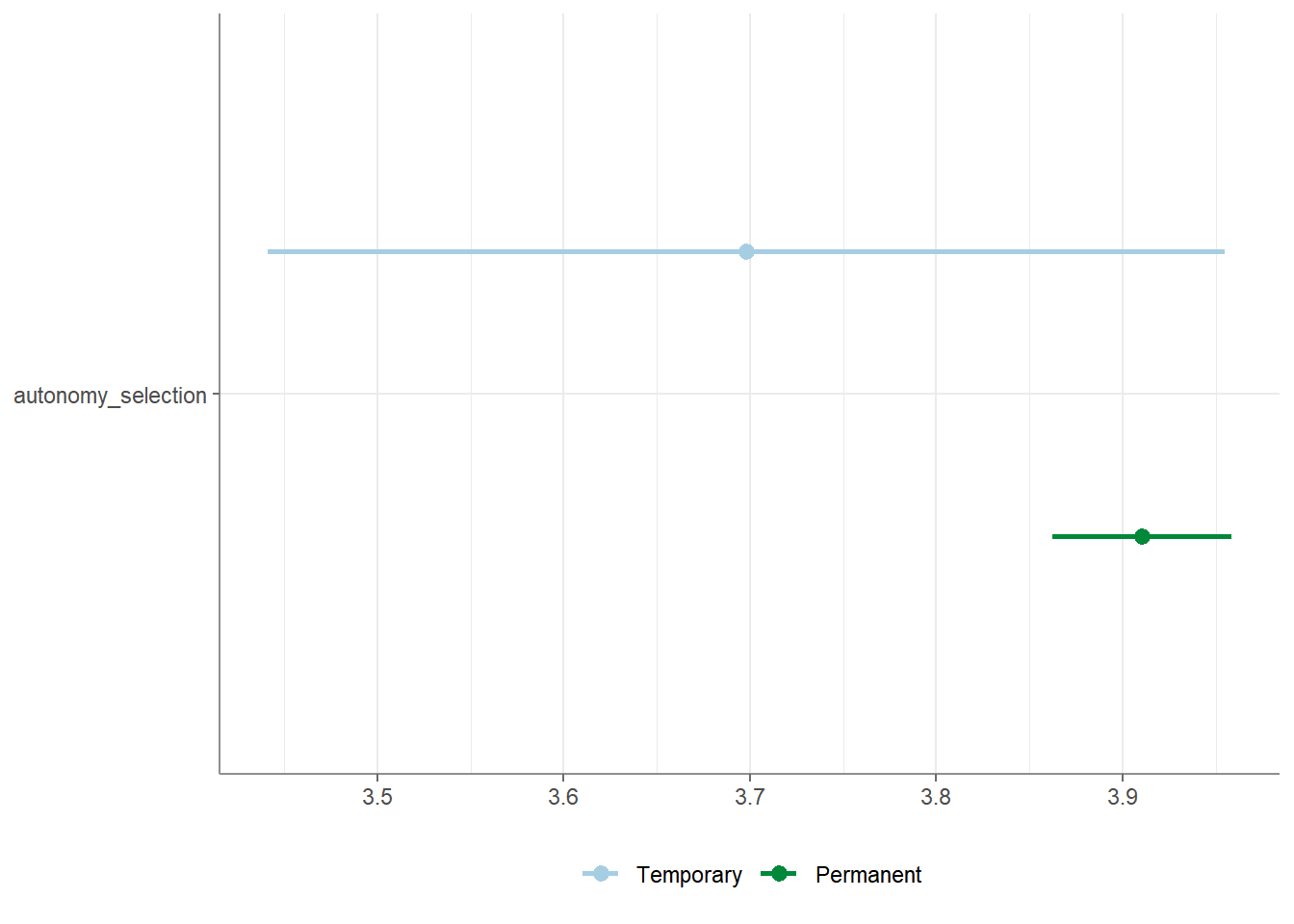
To access the full documentation / help:

?t_test()

8.4.3 unianova()

The unianova() function is used to compute one-way ANOVAs for one group variable and specified test variables. If no variables are specified, all numeric (integer or double) variables are used. Additionally, unianova() also conducts a Levene test just like the t_test() function to check the assumption of equal variances. If the data doesn’t meet this assumption, the function will switch to using Welch’s test.

For PostHoc tests, Tukey’s HSD is the default choice. However, if the assumption of equal variances isn’t met, the function will instead automatically use the Games-Howell test.

unianova works similarly to t_test(), i.e., you specify an independent (group) variable followed by one or more dependent variables.

WoJ %>% unianova(employment, autonomy_emphasis)
## # A tibble: 1 × 8
##   Variable                F df_num df_denom     p eta_squared Levene_p var_equal
## * <chr>             <num:.>  <dbl>    <dbl> <num>   <num:.3!>    <dbl> <chr>    
## 1 autonomy_emphasis   5.861      2     1192 0.003       0.010    0.175 TRUE

Provide only an independent variable to use all suitable variables in your data set as dependent variables:

WoJ %>% unianova(employment)
## # A tibble: 12 × 9
##    Variable           F df_num df_denom     p omega_squared eta_squared Levene_p
##  * <chr>         <num:>  <dbl>    <dbl> <num>     <num:.3!>   <num:.3!>    <dbl>
##  1 autonomy_sel…  2.012      2      251 0.136         0.002      NA        0    
##  2 autonomy_emp…  5.861      2     1192 0.003        NA           0.010    0.175
##  3 ethics_1       2.171      2     1197 0.115        NA           0.004    0.093
##  4 ethics_2       2.204      2     1197 0.111        NA           0.004    0.802
##  5 ethics_3       5.823      2      253 0.003         0.007      NA        0.001
##  6 ethics_4       3.453      2     1197 0.032        NA           0.006    0.059
##  7 work_experie…  3.739      2      240 0.025         0.006      NA        0.034
##  8 trust_parlia…  1.527      2     1197 0.218        NA           0.003    0.103
##  9 trust_govern… 12.864      2     1197 0.000        NA           0.021    0.083
## 10 trust_parties  0.842      2     1197 0.431        NA           0.001    0.64 
## 11 trust_politi…  0.328      2     1197 0.721        NA           0.001    0.58 
## 12 ethical_conc…  2.408      2     1197 0.090        NA           0.004    0.206
## # ℹ 1 more variable: var_equal <chr>

You can obtain the descriptives (mean and standard deviation for all group levels) by providing the additional argument descriptives = TRUE.

WoJ %>% unianova(employment, autonomy_emphasis, descriptives = TRUE)
## # A tibble: 1 × 14
##   Variable      F df_num df_denom     p eta_squared `M_Full-time` `SD_Full-time`
## * <chr>     <num>  <dbl>    <dbl> <num>   <num:.3!>         <dbl>          <dbl>
## 1 autonomy… 5.861      2     1192 0.003       0.010          4.12          0.781
## # ℹ 6 more variables: `M_Part-time` <dbl>, `SD_Part-time` <dbl>,
## #   M_Freelancer <dbl>, SD_Freelancer <dbl>, Levene_p <dbl>, var_equal <chr>

Similarly, you can retrieve PostHoc tests by providing the additional argument post_hoc = TRUE (default: Tukey’s HSD, otehrwise: Games-Howell). Please note that the post-hoc test results are best inspected by saving your analysis in a separate model and then using View(). Once View() has opened your model, you can navigate to the rightmost part and click on the 1 variable cell under the post hoc column. This will display your post hoc test results.

WoJ %>% unianova(employment, autonomy_emphasis, post_hoc = TRUE)
## # A tibble: 1 × 9
##   Variable       F df_num df_denom     p eta_squared post_hoc Levene_p var_equal
## * <chr>      <num>  <dbl>    <dbl> <num>   <num:.3!> <list>      <dbl> <chr>    
## 1 autonomy_… 5.861      2     1192 0.003       0.010 <df>        0.175 TRUE
# model2 <- WoJ %>% unianova(employment, autonomy_emphasis, post_hoc = TRUE)
# View(model2)

Alternatively, you can extract the PostHoc test results with this code:

WoJ %>%
  unianova(employment, autonomy_selection, post_hoc = TRUE) %>%
  dplyr::select(Variable, post_hoc) %>%
  tidyr::unnest(post_hoc)
## # A tibble: 3 × 11
##   Variable Group_Var contrast Delta_M conf_lower conf_upper     p       d     se
##   <chr>    <chr>     <chr>      <dbl>      <dbl>      <dbl> <dbl>   <dbl>  <dbl>
## 1 autonom… employme… Full-ti… -0.0780     -0.225     0.0688 0.422 -0.110  0.0440
## 2 autonom… employme… Full-ti… -0.139      -0.329     0.0512 0.199 -0.155  0.0569
## 3 autonom… employme… Part-ti… -0.0607     -0.284     0.163  0.798 -0.0729 0.0670
## # ℹ 2 more variables: t <dbl>, df <dbl>

If the variances are not equal, a Welch test (as an adaptation of the one-way ANOVA test) and a post hoc Games-Howell test will be performed automatically, replacing the classic ANOVA method:

WoJ %>% unianova(employment, autonomy_selection, descriptives = TRUE)
## # A tibble: 1 × 14
##   Variable                   F df_num df_denom     p omega_squared `M_Full-time`
## * <chr>              <num:.3!>  <dbl>    <dbl> <num>     <num:.3!>         <dbl>
## 1 autonomy_selection     2.012      2      251 0.136         0.002          3.90
## # ℹ 7 more variables: `SD_Full-time` <dbl>, `M_Part-time` <dbl>,
## #   `SD_Part-time` <dbl>, M_Freelancer <dbl>, SD_Freelancer <dbl>,
## #   Levene_p <dbl>, var_equal <chr>
WoJ %>%
  unianova(employment, autonomy_selection, post_hoc = TRUE) %>%
  dplyr::select(Variable, post_hoc) %>%
  tidyr::unnest(post_hoc)
## # A tibble: 3 × 11
##   Variable Group_Var contrast Delta_M conf_lower conf_upper     p       d     se
##   <chr>    <chr>     <chr>      <dbl>      <dbl>      <dbl> <dbl>   <dbl>  <dbl>
## 1 autonom… employme… Full-ti… -0.0780     -0.225     0.0688 0.422 -0.110  0.0440
## 2 autonom… employme… Full-ti… -0.139      -0.329     0.0512 0.199 -0.155  0.0569
## 3 autonom… employme… Part-ti… -0.0607     -0.284     0.163  0.798 -0.0729 0.0670
## # ℹ 2 more variables: t <dbl>, df <dbl>

Finally, you can visualize your test results by calling the visualize() function:

WoJ %>%
  unianova(employment, autonomy_emphasis) %>%
  visualize()

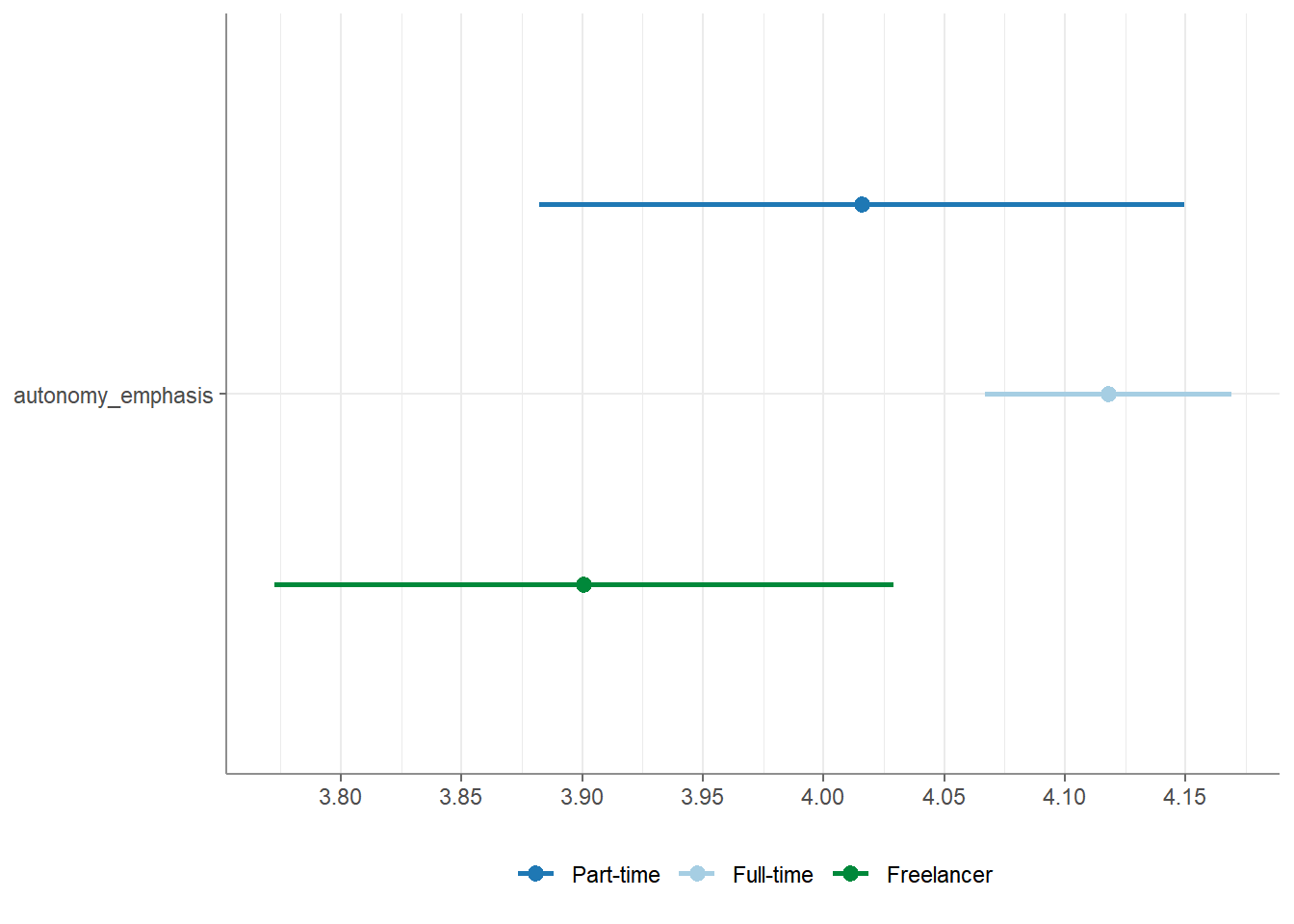
For full documentation / help:

?unianova()

8.4.4 correlate()

The correlate() function computes correlation coefficients for all combinations of the specified variables. If no variables are specified, all numeric (integer or double) variables are used.

WoJ %>% correlate(ethics_1, autonomy_selection)
## # A tibble: 1 × 6
##   x        y                        r    df       p     n
## * <chr>    <chr>                <dbl> <int>   <dbl> <int>
## 1 ethics_1 autonomy_selection -0.0766  1195 0.00798  1197

Once again, you can specify more than two variables:

WoJ %>% correlate(ethics_1, autonomy_selection, work_experience)
## # A tibble: 3 × 6
##   x                  y                        r    df            p     n
## * <chr>              <chr>                <dbl> <int>        <dbl> <int>
## 1 ethics_1           autonomy_selection -0.0766  1195 0.00798       1197
## 2 ethics_1           work_experience    -0.103   1185 0.000387      1187
## 3 autonomy_selection work_experience     0.161   1182 0.0000000271  1184

Three variables? That screams “partial correlation” to me! If you’d like to calculate the partial correlation coefficient of three variables, just add the optional parameter partial =.

WoJ %>% correlate(ethics_1, autonomy_selection, partial = work_experience)
## # A tibble: 1 × 7
##   x        y                  z                     r    df      p     n
## * <chr>    <chr>              <chr>             <dbl> <dbl>  <dbl> <int>
## 1 ethics_1 autonomy_selection work_experience -0.0619  1181 0.0332  1184

And you can get the correlation for all suitable variables in your data set:

WoJ %>% correlate()
## # A tibble: 66 × 6
##    x                  y                        r    df         p     n
##  * <chr>              <chr>                <dbl> <int>     <dbl> <int>
##  1 autonomy_selection autonomy_emphasis  0.644    1192 4.83e-141  1194
##  2 autonomy_selection ethics_1          -0.0766   1195 7.98e-  3  1197
##  3 autonomy_selection ethics_2          -0.0274   1195 3.43e-  1  1197
##  4 autonomy_selection ethics_3          -0.0257   1195 3.73e-  1  1197
##  5 autonomy_selection ethics_4          -0.0781   1195 6.89e-  3  1197
##  6 autonomy_selection work_experience    0.161    1182 2.71e-  8  1184
##  7 autonomy_selection trust_parliament  -0.00840  1195 7.72e-  1  1197
##  8 autonomy_selection trust_government   0.0414   1195 1.53e-  1  1197
##  9 autonomy_selection trust_parties      0.0269   1195 3.52e-  1  1197
## 10 autonomy_selection trust_politicians  0.0109   1195 7.07e-  1  1197
## # ℹ 56 more rows

Specify a focus variable using the with parameter to correlate all other variables with this focus variable.

WoJ %>% 
  correlate(autonomy_selection, autonomy_emphasis, with = work_experience)
## # A tibble: 2 × 6
##   x               y                      r    df            p     n
## * <chr>           <chr>              <dbl> <int>        <dbl> <int>
## 1 work_experience autonomy_selection 0.161  1182 0.0000000271  1184
## 2 work_experience autonomy_emphasis  0.155  1180 0.0000000887  1182

You might want to turn these correlations into an advanced correlation matrix, just like you find them in SPSS. You can do that using an additional function to_correlation_matrix after your correlate() function:

WoJ %>%
  correlate() %>%
  to_correlation_matrix()
## # A tibble: 12 × 13
##    r             autonomy_selection autonomy_emphasis ethics_1 ethics_2 ethics_3
##  * <chr>                      <dbl>             <dbl>    <dbl>    <dbl>    <dbl>
##  1 autonomy_sel…            1                 0.644   -0.0766  -0.0274   -0.0257
##  2 autonomy_emp…            0.644             1       -0.114   -0.0337   -0.0297
##  3 ethics_1                -0.0766           -0.114    1        0.172     0.165 
##  4 ethics_2                -0.0274           -0.0337   0.172    1         0.409 
##  5 ethics_3                -0.0257           -0.0297   0.165    0.409     1     
##  6 ethics_4                -0.0781           -0.127    0.343    0.321     0.273 
##  7 work_experie…            0.161             0.155   -0.103   -0.168    -0.0442
##  8 trust_parlia…           -0.00840          -0.00465 -0.0378   0.00161  -0.0486
##  9 trust_govern…            0.0414            0.0268  -0.102    0.0374   -0.0743
## 10 trust_parties            0.0269            0.0102  -0.0472   0.0238   -0.0115
## 11 trust_politi…            0.0109            0.00242 -0.00725  0.0250   -0.0212
## 12 ethical_conc…           -0.0738           -0.108    0.555    0.734     0.687 
## # ℹ 7 more variables: ethics_4 <dbl>, work_experience <dbl>,
## #   trust_parliament <dbl>, trust_government <dbl>, trust_parties <dbl>,
## #   trust_politicians <dbl>, ethical_concerns <dbl>

Of course, you can change the correlation method:

  1. Using Pearson’s r (default):
WoJ %>% correlate(ethics_1, autonomy_selection, method = "pearson")
## # A tibble: 1 × 6
##   x        y                        r    df       p     n
## * <chr>    <chr>                <dbl> <int>   <dbl> <int>
## 1 ethics_1 autonomy_selection -0.0766  1195 0.00798  1197
  1. Using Spearman’s rho:
WoJ %>% correlate(ethics_1, autonomy_selection, method = "spearman")
## # A tibble: 1 × 6
##   x        y                      rho df         p     n
## * <chr>    <chr>                <dbl> <lgl>  <dbl> <int>
## 1 ethics_1 autonomy_selection -0.0716 NA    0.0132  1197
  1. Using Kendall’s tau:
WoJ %>% correlate(ethics_1, autonomy_selection, method = "kendall")
## # A tibble: 1 × 6
##   x        y                      tau df         p     n
## * <chr>    <chr>                <dbl> <lgl>  <dbl> <int>
## 1 ethics_1 autonomy_selection -0.0646 NA    0.0130  1197

Finally, you can visualize your test results by calling the visualize() function. Based on your input variables and whether you want to visualize a partial correlation, the choice of graph might vary:

  1. Visualize a bivariate correlation:
WoJ %>%
  correlate(ethics_1, autonomy_selection) %>%
  visualize()

# Pro tip: use parameters which = jitter and which = alpha to change layout of the geom_points
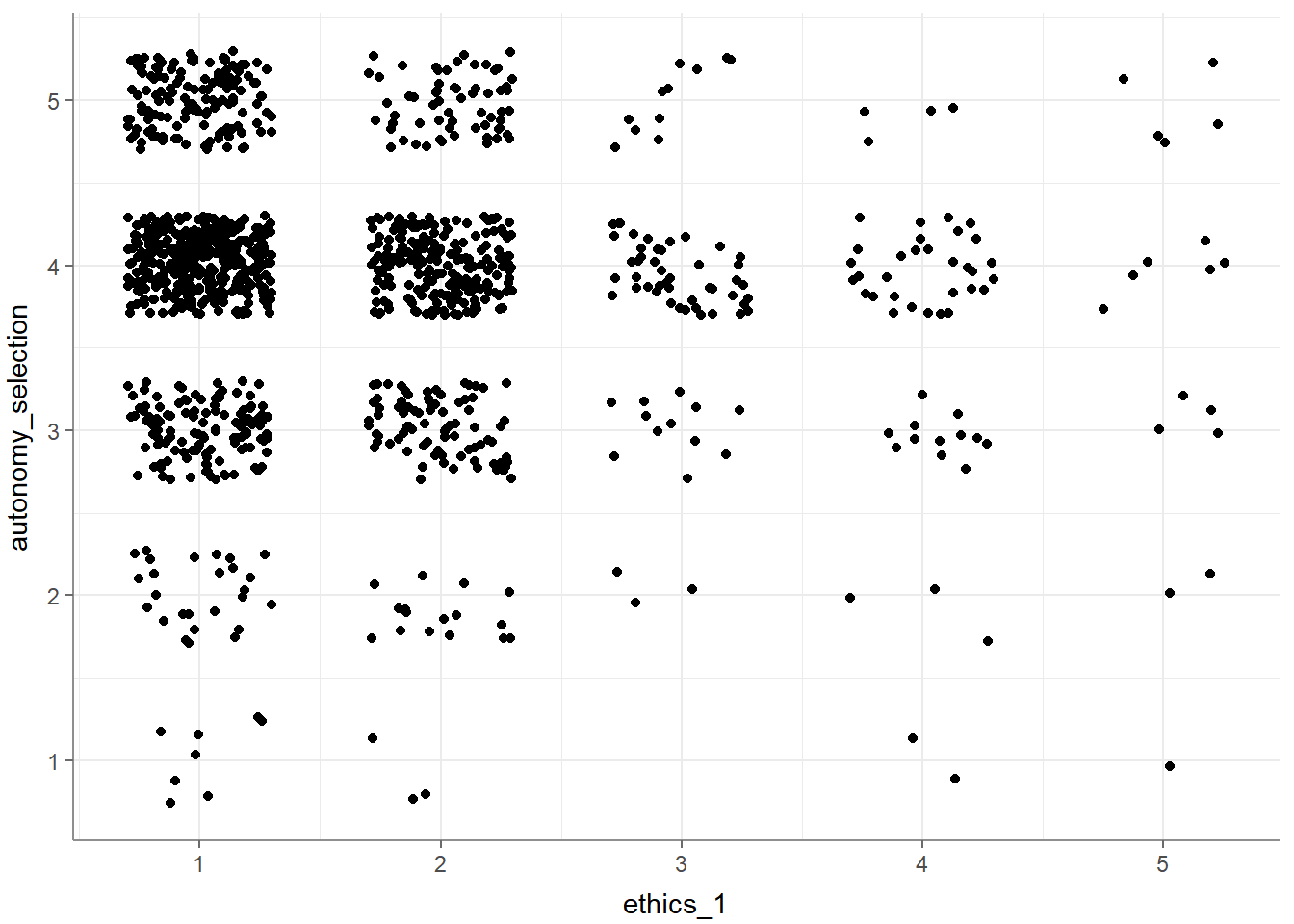
  1. Visualize with multiple variables:
WoJ %>%
  correlate(ethics_1, autonomy_selection, work_experience) %>%
  visualize()

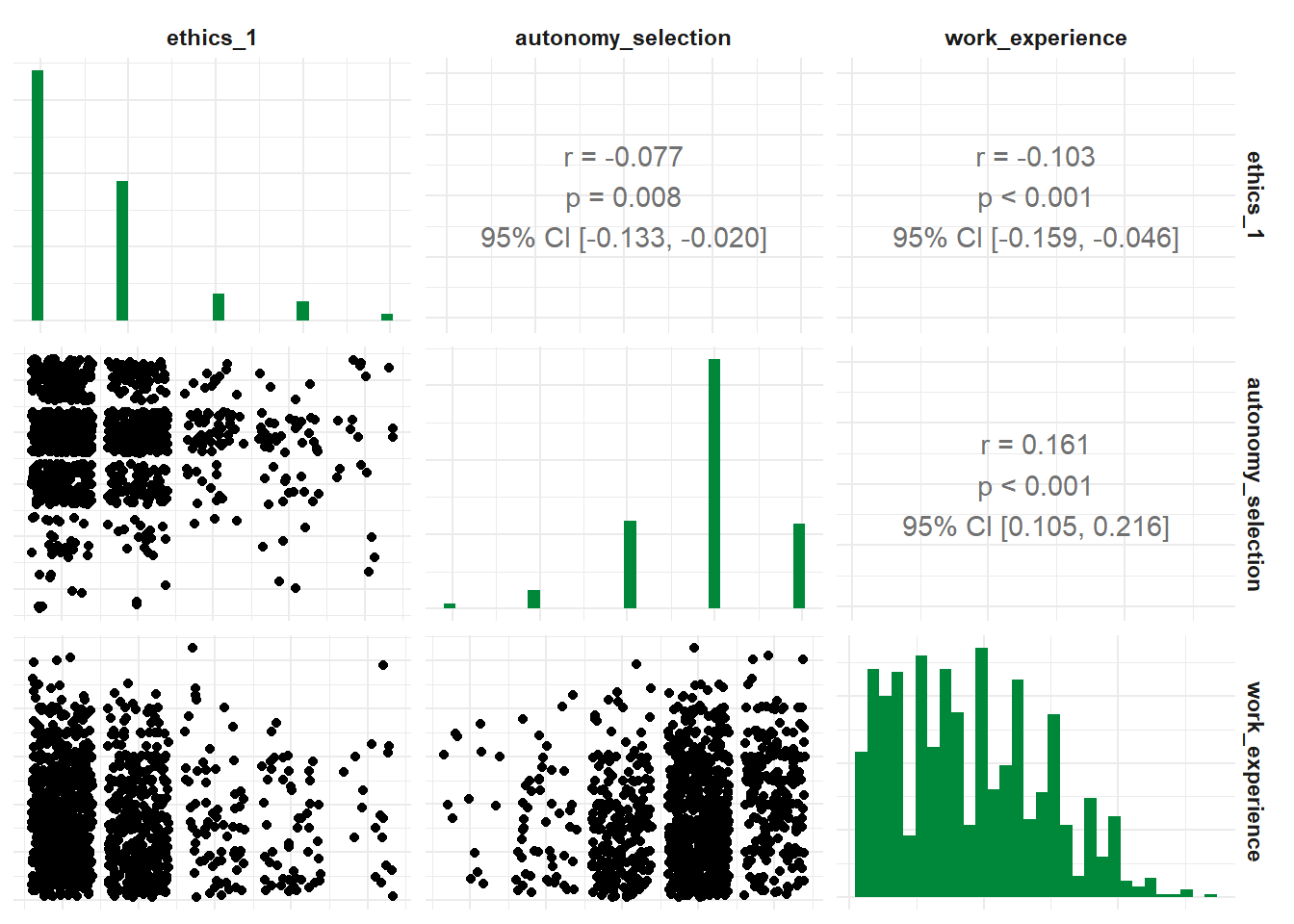
  1. Visualize a partial correlation:
WoJ %>%
  correlate(ethics_1, autonomy_selection, partial = work_experience) %>%
  visualize()

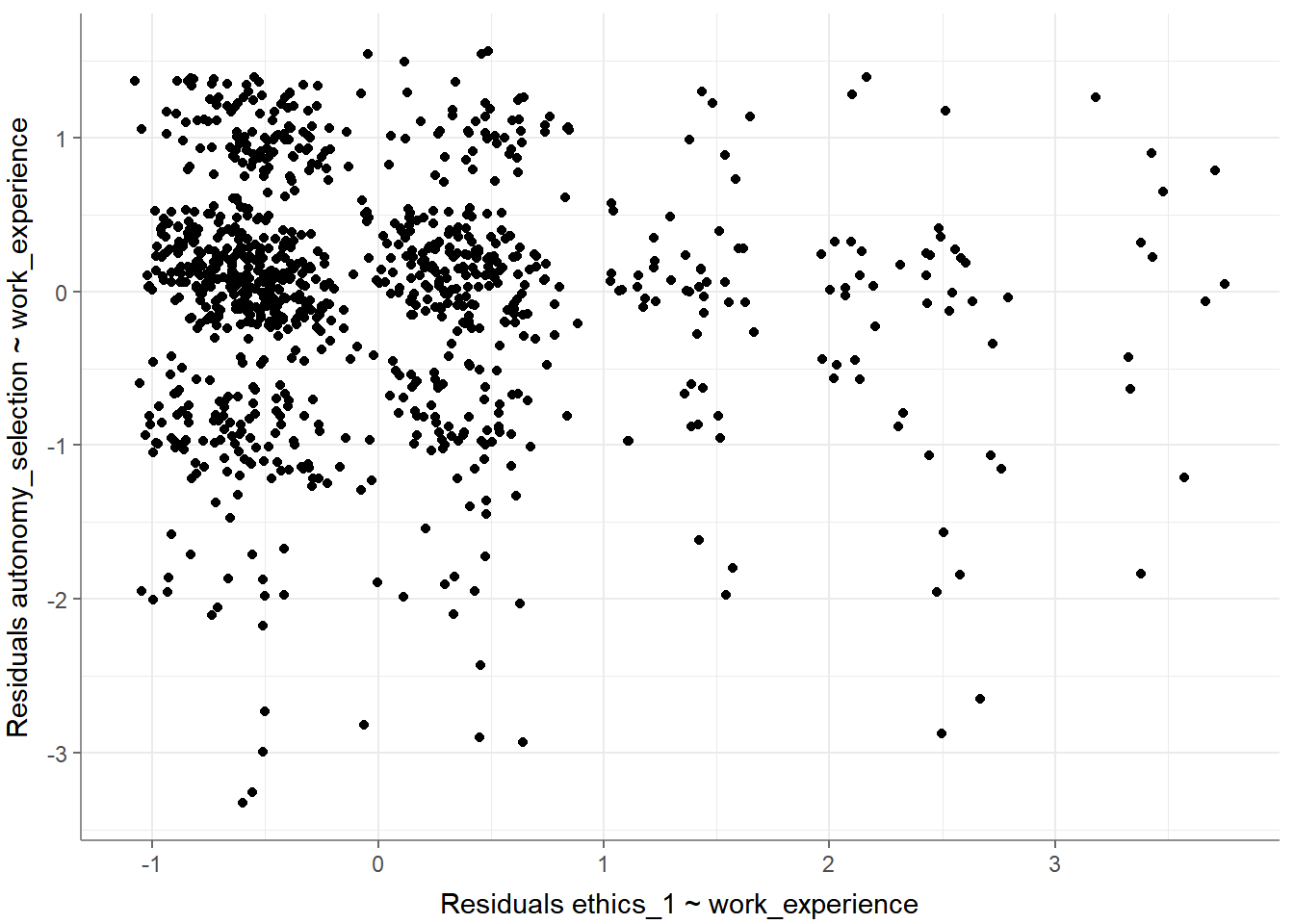
Of course, you can always get help:

?correlate()

8.4.5 regress()

Finally, you can also run linear regressions. The regress() function will compute a linear regression for all independent variables on the specified dependent variable.

WoJ %>% regress(ethics_1, autonomy_selection, work_experience)
## # A tibble: 3 × 6
##   Variable                  B  StdErr    beta     t        p
## * <chr>                 <dbl>   <dbl>   <dbl> <dbl>    <dbl>
## 1 (Intercept)         2.03    0.129   NA      15.8  5.32e-51
## 2 autonomy_selection -0.0692  0.0325  -0.0624 -2.13 3.32e- 2
## 3 work_experience    -0.00762 0.00239 -0.0934 -3.19 1.46e- 3
## # F(2, 1181) = 8.677001, p = 0.000182, R-square = 0.014482

You can also perform a linear modeling of multiple independent variables (this will use stepwise regression modeling):

WoJ %>% regress(ethics_1, autonomy_selection, work_experience)
## # A tibble: 3 × 6
##   Variable                  B  StdErr    beta     t        p
## * <chr>                 <dbl>   <dbl>   <dbl> <dbl>    <dbl>
## 1 (Intercept)         2.03    0.129   NA      15.8  5.32e-51
## 2 autonomy_selection -0.0692  0.0325  -0.0624 -2.13 3.32e- 2
## 3 work_experience    -0.00762 0.00239 -0.0934 -3.19 1.46e- 3
## # F(2, 1181) = 8.677001, p = 0.000182, R-square = 0.014482

You can even check the preconditions of a linear regression (e.g., multicollinearity and homoscedasticity) by providing optional arguments / parameters:

WoJ %>% regress(ethics_1, autonomy_selection, work_experience,
  check_independenterrors = TRUE,
  check_multicollinearity = TRUE,
  check_homoscedasticity = TRUE
)
## # A tibble: 3 × 8
##   Variable                  B  StdErr    beta     t        p   VIF tolerance
## * <chr>                 <dbl>   <dbl>   <dbl> <dbl>    <dbl> <dbl>     <dbl>
## 1 (Intercept)         2.03    0.129   NA      15.8  5.32e-51 NA       NA    
## 2 autonomy_selection -0.0692  0.0325  -0.0624 -2.13 3.32e- 2  1.03     0.974
## 3 work_experience    -0.00762 0.00239 -0.0934 -3.19 1.46e- 3  1.03     0.974
## # F(2, 1181) = 8.677001, p = 0.000182, R-square = 0.014482
## - Check for independent errors: Durbin-Watson = 2.037690 (p = 0.554000)
## - Check for homoscedasticity: Breusch-Pagan = 6.966472 (p = 0.008305)
## - Check for multicollinearity: VIF/tolerance added to output

Or you can make visual inspections to check the preconditions using several different visualizations:

  1. Base visualization:
WoJ %>%
  regress(ethics_1, autonomy_selection, work_experience) %>%
  visualize()

# Pro tip: use parameters which = jitter and which = alpha to change layout of the geom_points
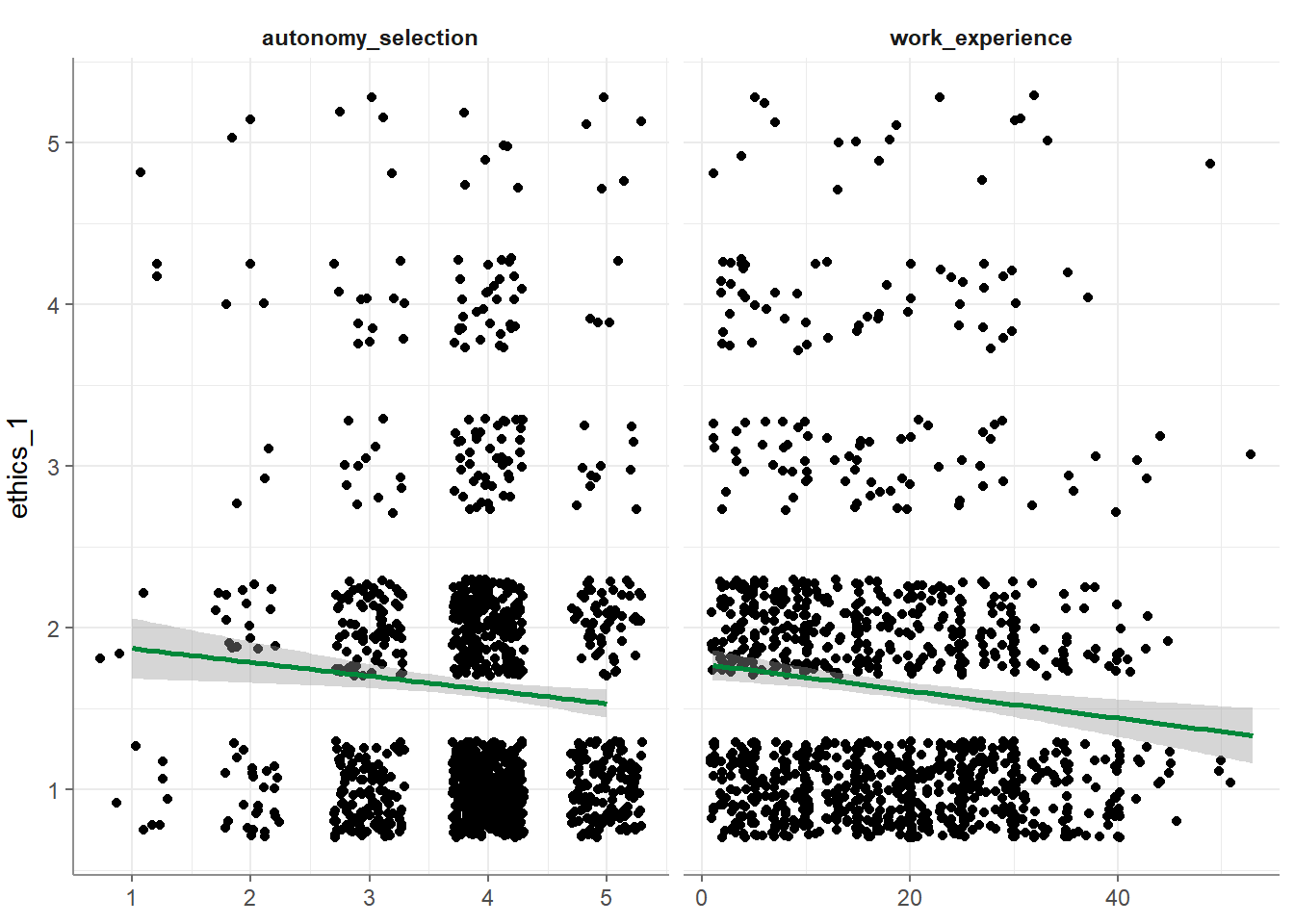
  1. Correlograms among independent variables:
WoJ %>%
  regress(ethics_1, autonomy_selection, work_experience) %>%
  visualize(which = "correlogram")

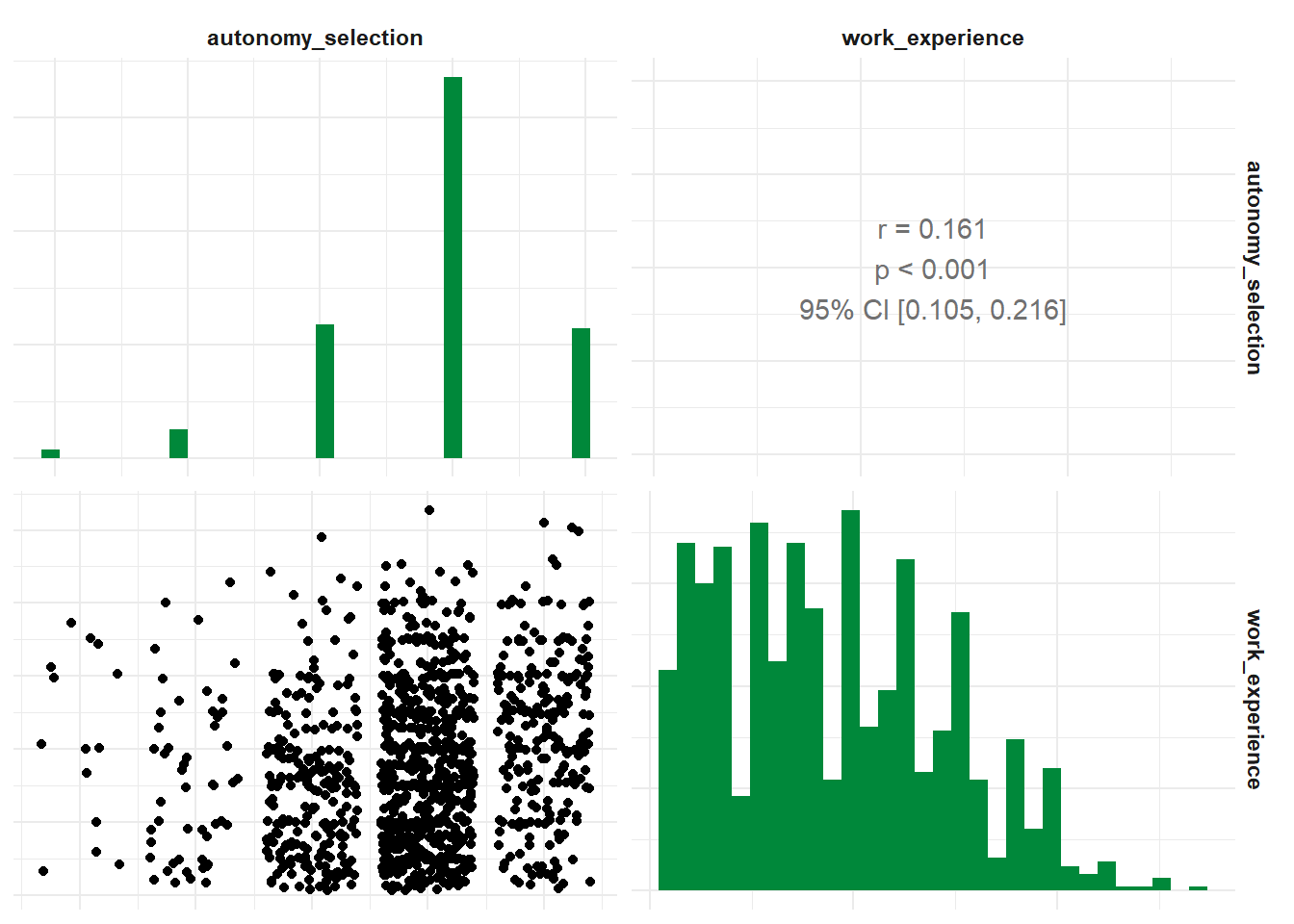
  1. Residuals-versus-fitted plot to determine distributions:
WoJ %>%
  regress(ethics_1, autonomy_selection, work_experience) %>%
  visualize(which = "resfit")

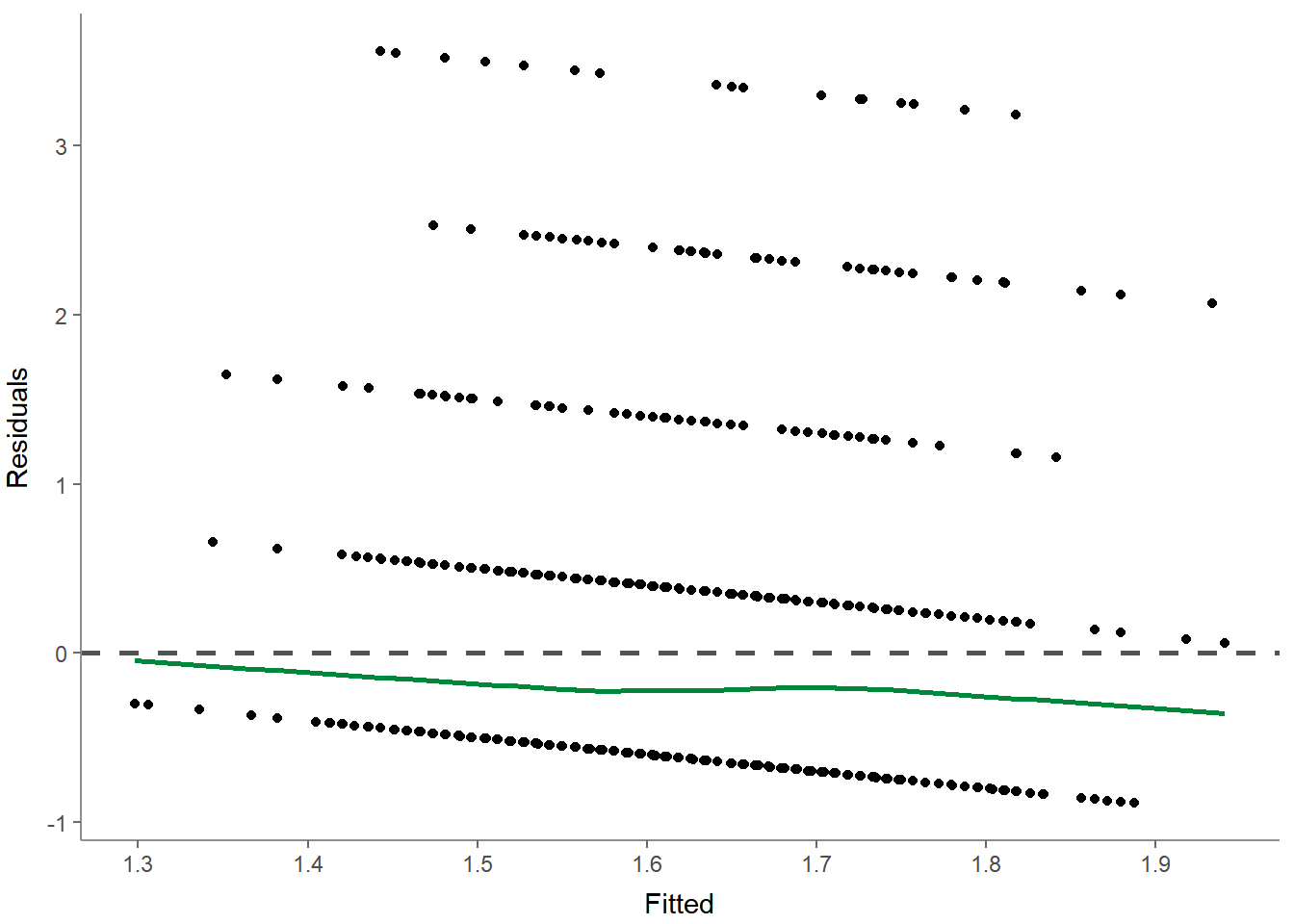
  1. Normal probability-probability plot to check for multicollinearity:
WoJ %>%
  regress(ethics_1, autonomy_selection, work_experience) %>%
  visualize(which = "pp")

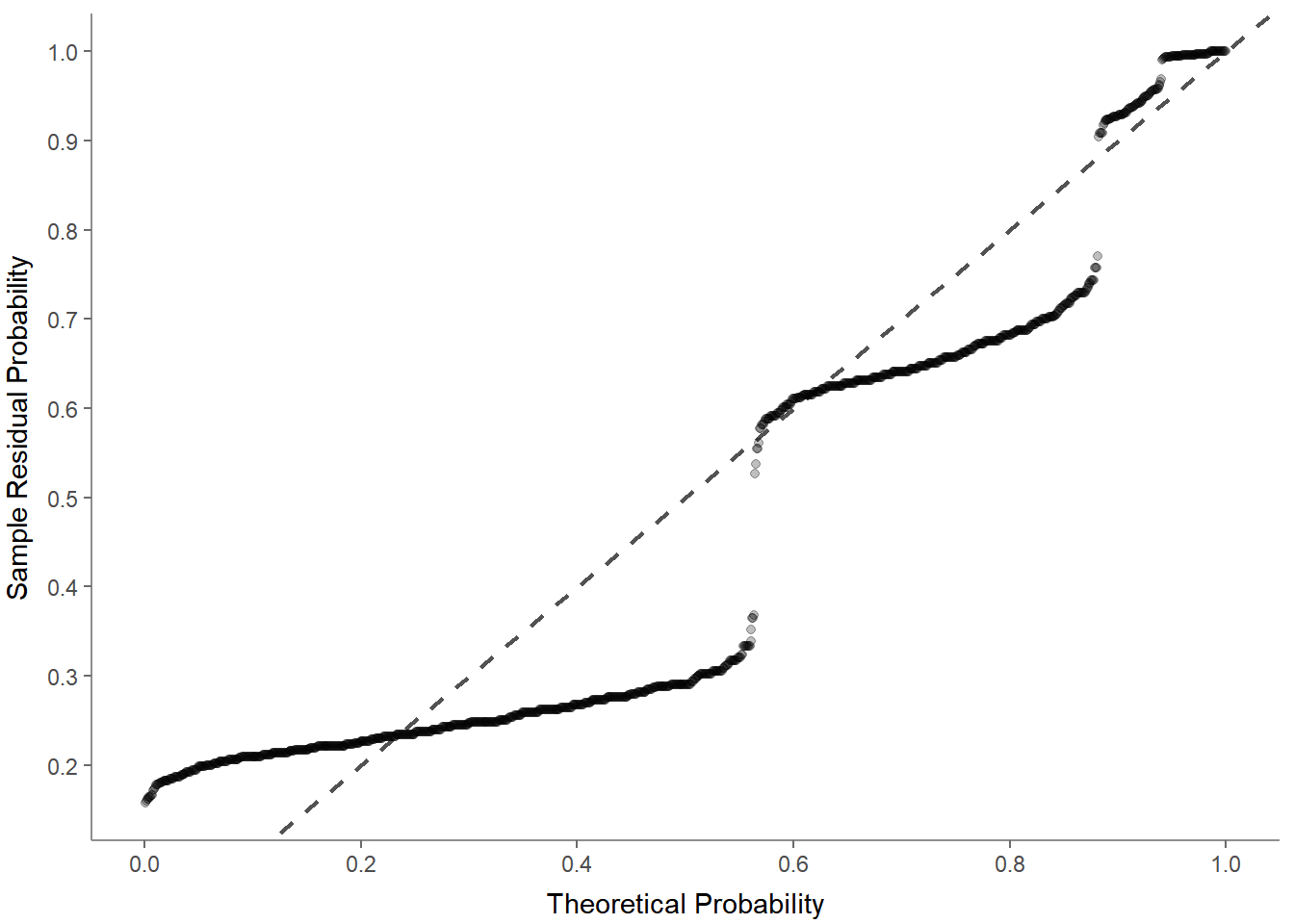
  1. Scale-location (sometimes also called spread-location) plot to check whether residuals are spread equally (to help check for homoscedasticity):
WoJ %>%
  regress(ethics_1, autonomy_selection, work_experience) %>%
  visualize(which = "scaloc")

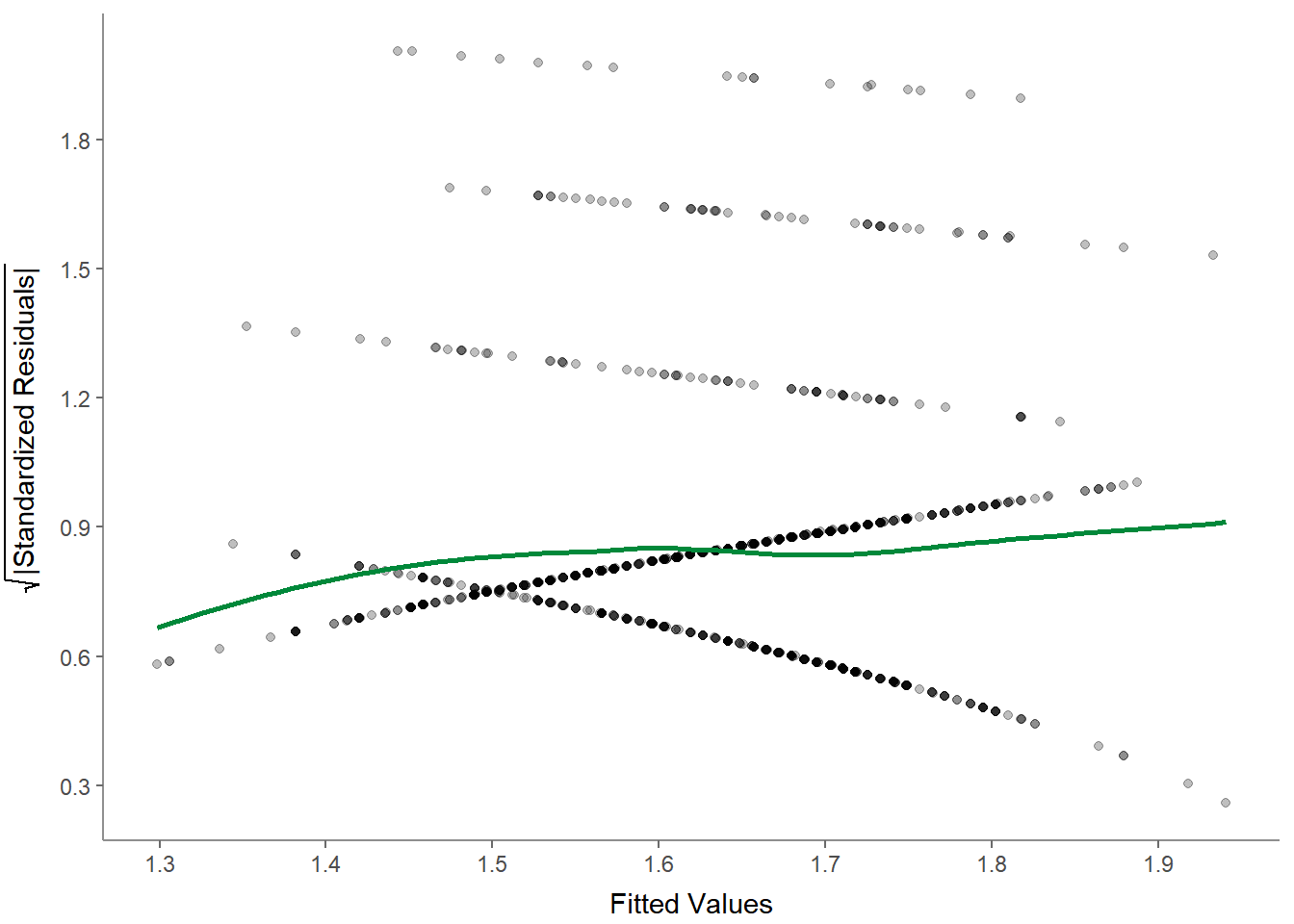
  1. Residuals-versus-leverage plot to check for influential outliers affecting the final model more than the rest of the data:
WoJ %>%
  regress(ethics_1, autonomy_selection, work_experience) %>%
  visualize(which = "reslev")

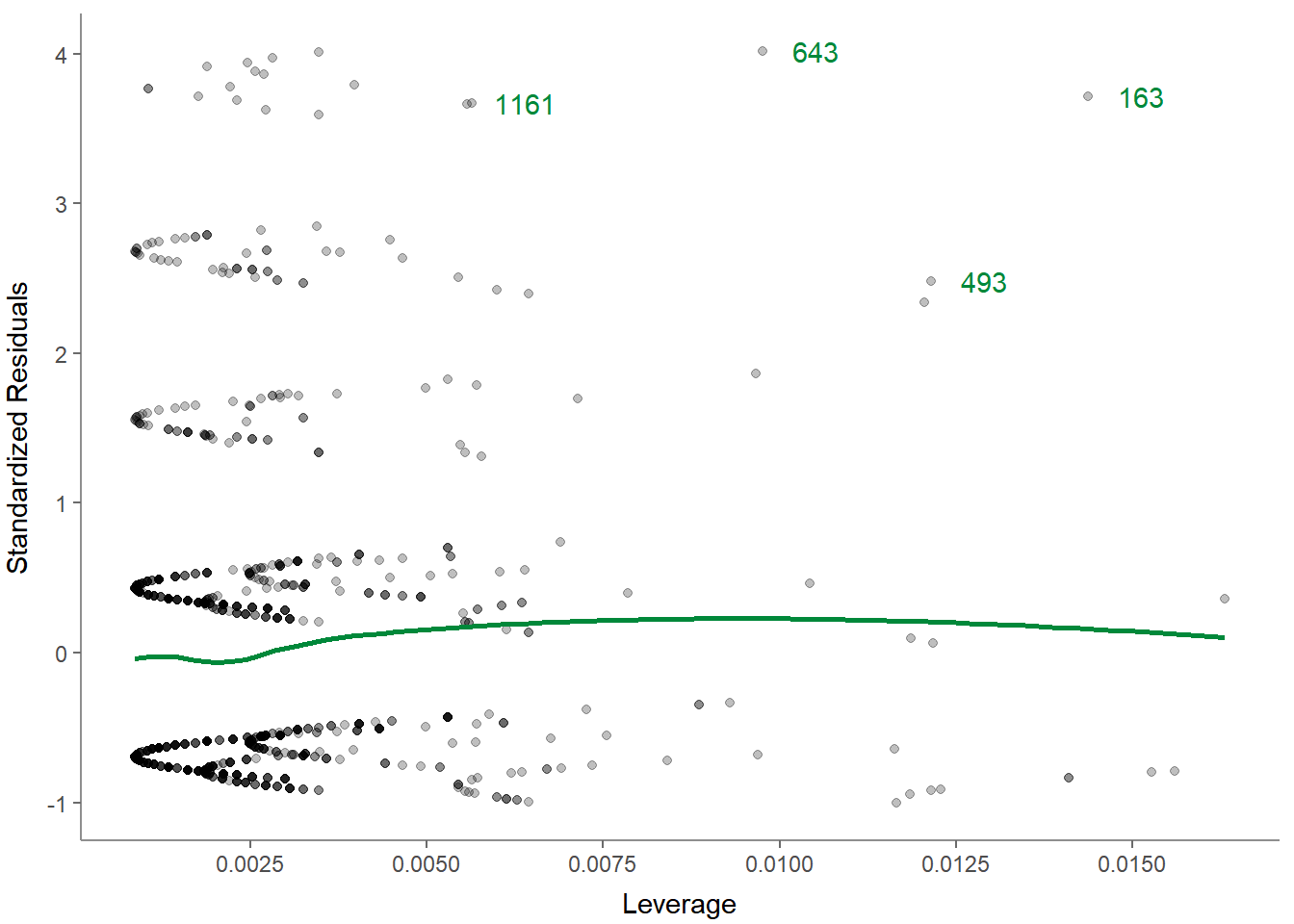
Again, you can always get help:

?regress()

And if you need help to interpret the regression plots, you can look up the help of visualize() and scroll down until you reach regress():

?tidycomm::visualize()

We are done with our tutorial about data analysis! Let’s have a final exercise to repeat what we’ve learned: Exercise 6: dplyr, ggplot, tidycomm.